Hidden Rectangles – The Void Paradox

Dear readers, welcome to a fascinating journey through the world of mathematics, where every curve hides a secret and every rectangle tells a story. Imagine having to calculate the work done by a variable force, analyze the diffusion of a drug in the blood, or measure the growth of a population over time. Have you ever wondered how these problems could be tackled? Today we will discover together how the sum of the areas of rectangles can help us answer these questions, revealing the area under a curve. This concept, simple but revolutionary, has forever changed our understanding of the natural world.

The Magic of Rectangles: A Journey through the History of Mathematics

Imagine standing before a beautiful mountainous landscape. The peaks follow one another gently, creating a sinuous profile that fascinates the eye. Now, think of wanting to measure the total area covered by this panorama. How would you do it? Here comes into play one of the simplest yet most ingenious ideas in mathematics: the sum of the areas of rectangles to approximate the area under a curve.

This method, known as the Riemann sum, is named after the great German mathematician Bernhard Riemann. Born in 1826, Riemann made significant contributions to many areas of mathematics, but he is perhaps most famous for his work on integration.

An Anecdote from Riemann’s Life

Riemann was known for his deep thinking and his ability to see connections that eluded others. One of the most famous stories tells how, as a young student, he had the habit of walking along the paths of the German countryside, reflecting on how nature could be described through mathematics. It is said that during one of these walks, he had the intuition that led him to develop the concept of the Riemann sum.

How Does the Riemann Sum Work?

To better understand this concept, let’s imagine wanting to calculate the area under a curve that represents the path of a mountain. We divide the interval along the x-axis into equal segments and draw rectangles under the curve, with the base of each rectangle coinciding with a segment and the height touching the curve.

Parabola Example

Considering the parabola $y = x^2$ inside [0, 1]. We divide this interval into n equal parts of length $\Delta x = \frac{1}{n}$ . The Riemann sum can be expressed as:

$S = \sum_{i=1}^{n} f(x_i) \Delta x$

where $x_i$ is a point in the interval $[x_{i-1}, x_i]$ . In this case, we can choose $x_i = \frac{i}{n}$ . herefore, the calculation of the Riemann sum becomes:

$S = \sum_{i=1}^{n} \left( \frac{i}{n} \right)^2 \cdot \frac{1}{n} = \sum_{i=1}^{n} \frac{i^2}{n^3} = \frac{1}{n^3} \sum_{i=1}^{n} i^2$

Using the formula for the sum of the squares of the first n integers:

$\sum_{i=1}^{n} i^2 = \frac{n(n+1)(2n+1)}{6}$

we get:

$S = \frac{1}{n^3} \cdot \frac{n(n+1)(2n+1)}{6} = \frac{(n+1)(2n+1)}{6n^2}$

As $n$ tends to infinity, this sum approaches the integral:

$\int_0^1 x^2 \, dx = \left[ \frac{x^3}{3} \right]_0^1 = \frac{1}{3}$

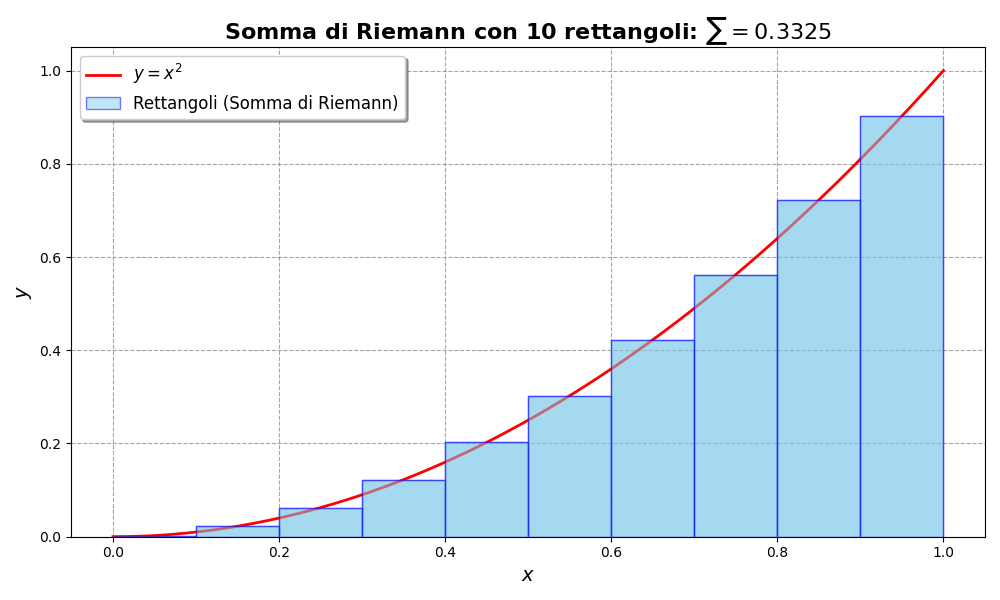
Graph of the Riemann Sum for a Parabola

To better visualize this concept, we can see how the rectangles behave under the curve of the parabola $y = x^2$ when we increase the number of subdivisions $n$ using this small customizable script executable directly from a browser at Python-Fiddle.

import matplotlib.pyplot as plt
import numpy as np

# Funzione della parabola
def f(x):
    return x**2

# Intervallo di integrazione
a, b = 0, 1
n = 10  # Numero di rettangoli

# Larghezza dei rettangoli
dx = (b - a) / n

# Punti di valutazione
x = np.linspace(a, b, n+1)
y = f(x)

# Sommando le aree dei rettangoli
x_mid = (x[:-1] + x[1:]) / 2
y_mid = f(x_mid)
sum_rectangles = np.sum(y_mid * dx)

# Creazione del grafico
x_vals = np.linspace(a, b, 1000)
y_vals = f(x_vals)

plt.plot(x_vals, y_vals, 'r', label='')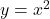
plt.bar(x_mid, y_mid, width=dx, alpha=0.5, edgecolor='b', label='Rettangoli (Somma di Riemann)')
plt.title(f'Somma di Riemann con {n} rettangoli: ')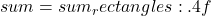
plt.xlabel('')
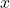plt.ylabel('')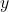
plt.legend()
plt.show()

HomeMade Experiment

For the more curious ones, here is a simple experiment you can try at home. Draw a curve on a sheet of paper and divide the area under it into small rectangles, calculating their areas and summing them up. Then compare this sum with the result obtained using smaller rectangles. You will discover how precise this technique can be and how fascinating mathematics is!

The Riemann sum teaches us that even the simplest ideas can lead to great discoveries. The next time you admire a landscape or ponder a complex problem, remember that behind every curve lies a story, and that mathematics is the tool that allows us to tell it. Thank you for joining us on this fascinating journey; until the next discovery!

Here, dear readers, is a small window into the wonder of mathematical thought. Keep exploring, asking questions, and being fascinated by the answers that science has to offer.

cyb3rdm0n