Magnificent readers, today I want to take you on a fascinating journey through the Matrix… just kidding, BAZINGA!

…I will guide you through the history of information theory, a field that has radically transformed our ability to communicate in the modern world. This journey would not be possible without the extraordinary contributions of two giants: Harry Nyquist and Claude Shannon. Their theorems are the cornerstone of our understanding of how information can be transmitted and reconstructed through communication channels.
Nyquist Sampling Theorem
Harry Nyquist, an engineer at Bell Telephone Laboratories, in 1928 formulated a crucial principle for the transmission of information through bandwidth-limited channels. The Nyquist Sampling Theorem states that for a band-limited analog signal, the sampling frequency must be at least twice the maximum frequency present in the signal for the signal to be completely reconstructed without loss of information..
Statement of Nyquist Theorem
For a signal with maximum frequency ![]() , the sampling frequency
, the sampling frequency ![]() must satisfy:
must satisfy:![]()
This minimum sampling frequency is known as the Nyquist frequency. If the signal is sampled at a frequency lower than the Nyquist frequency, the phenomenon of aliasing occurs, where high-frequency components overlap with low-frequency ones, causing irreversible distortions in the reconstructed signal.
Shannon Channel Capacity Theorem
Claude Shannon, often called the father of information theory, in 1948 formalized the concepts that describe the maximum amount of information that can be transmitted through a noisy communication channel. The Shannon Channel Capacity Theorem sets an upper limit (channel capacity) to the rate of information transmission beyond which the transmission inevitably becomes error-prone

Statement of Shannon Theorem
The capacity ![]() of a channel with bandwidth
of a channel with bandwidth ![]() and signal-to-noise ratio
and signal-to-noise ratio ![]() is given by:
is given by:![]()
where:
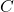 is the channel capacity in bits per second
is the channel capacity in bits per second 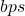 ,
,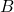 is the channel bandwidth in hertz (
is the channel bandwidth in hertz (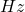 ),
),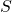 is the signal power,
is the signal power,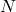 is the noise power..
is the noise power..
Relationship between Nyquist and Shannon Theorems
The Nyquist and Shannon theorems are closely related and complementary. While the Nyquist theorem focuses on sampling and reconstructing analog signals, the Shannon theorem deals with the data transmission capacity through noisy channels.
Sampling and Transmission: The Nyquist theorem lays the foundation for sampling analog signals, a necessary preliminary step for digitization. Once the signal is sampled, the Shannon theorem provides guidelines for efficient digital data transmission.
Aliasing and Channel Capacity: The Nyquist theorem prevents aliasing, ensuring that signals can be reconstructed without errors. Subsequently, the Shannon theorem ensures that digital data can be transmitted through a channel without exceeding the channel’s capacity, minimizing errors.
Complete Example: Digitization of an Audio Signal
The digitization of an audio signal follows fundamental principles of information theory developed by Nyquist and Shannon..
Step 1: Sampling the Audio Signal
Sampling means taking regular measurements of a continuous signal to convert it into a digital format.
- Determining the Maximum Frequency of the Signal:
Maximum frequencies audible by the human ear: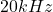 .
. - Calculating the Sampling Frequency:
According to the Nyquist theorem: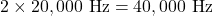 .
.
In practice, a frequency of is used, standard for audio CDs.
is used, standard for audio CDs. - Sampling the Signal:
Recording the signal value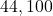 times per second.
times per second.
Step 2: Quantizing the Samples
Quantizing means transforming each continuous sample into a discrete value.
- 16-Bit Quantization:
Each sample is rounded to one of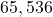 possible values (
possible values (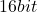 ).
).
Step 3: Encoding the Signal: Encoding means transforming the quantized samples into a digital format for storage or transmission.
- Calculating the Bit Rate:
Sampling frequency of and quantization at
and quantization at 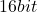 :
:
Step 4: Transmitting the Signal:
To transmit the digitized audio signal, we consider Shannon’s Channel Capacity.
- Determining the Bandwidth and Signal-to-Noise Ratio (SNR):
Bandwidth of and SNR of
and SNR of  .
. - Calculating the Channel Capacity:
Maximum channel capacity is
- Verifying the Transmission Rate:
Our signal requires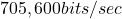 , higher than the channel capacity. Data compression or channel quality improvement is necessary.
, higher than the channel capacity. Data compression or channel quality improvement is necessary.
Conclusions
The contributions of Harry Nyquist and Claude Shannon have revolutionized the way we think and operate with information. Their theorems represent the foundations upon which digitization, transmission, and storage of information in the modern world are based. For engineers and scientists in the fields of telecommunications, computer science, and information technologies, understanding and applying these principles is not only essential but also a continual source of inspiration.
It is fascinating to remember that Claude Shannon, besides his pioneering studies, was also a man of many curiosities. He loved building mechanical devices in his spare time, such as a carousel of gyroscopes in his living room and a mechanical mouse capable of finding cheese in a maze. These hobbies reflected the same ingenuity and creativity that characterized his scientific research.
Dear readers, information theory is a field that continues to evolve and shape our daily lives in surprising and extraordinary ways. I invite you to further explore these fascinating principles because only through knowledge can we understand and appreciate the complexity of the world around us. Happy studying to all!
