Rettangoli Nascosti – The Void Paradox

Cari lettori, benvenuti in un viaggio affascinante attraverso il mondo della matematica, dove ogni curva cela un segreto e ogni rettangolo racconta una storia. Immaginate di dover calcolare il lavoro compiuto da una forza variabile, di analizzare la diffusione di un farmaco nel sangue o di misurare la crescita di una popolazione nel tempo. Vi siete mai chiesti come si potrebbero affrontare questi problemi? Oggi scopriremo insieme come la somma delle aree dei rettangoli possa aiutarci a rispondere a queste domande, rivelando l’area sotto una curva. Questo concetto, semplice ma rivoluzionario, ha cambiato per sempre la nostra comprensione del mondo naturale.

La Magia dei Rettangoli: Un Viaggio nella Storia della Matematica

Immaginate di trovarvi davanti a un bellissimo paesaggio montuoso. Le vette si susseguono dolcemente, creando un profilo sinuoso che affascina lo sguardo. Ora, pensate di voler misurare l’area totale coperta da questo panorama. Come fare? Ecco che entra in gioco una delle idee più semplici ma geniali della matematica: la somma delle aree di rettangoli per approssimare l’area sotto una curva.

Questo metodo, noto come somma di Riemann, prende il nome dal grande matematico tedesco Bernhard Riemann. Nato nel 1826, Riemann ha contribuito in modo significativo a molte aree della matematica, ma è forse più famoso per il suo lavoro sull’integrazione.

Un Aneddoto dalla Vita di Riemann

Riemann era noto per il suo pensiero profondo e la sua capacità di vedere connessioni che sfuggivano ad altri. Una delle storie più famose racconta di come, da giovane studente, avesse l’abitudine di camminare lungo i sentieri delle campagne tedesche, riflettendo su come la natura potesse essere descritta attraverso la matematica. Si dice che proprio durante una di queste passeggiate abbia avuto l’intuizione che lo portò a sviluppare il concetto di somma di Riemann.

Come Funziona la Somma di Riemann?

Per capire meglio questo concetto, immaginiamo di voler calcolare l’area sotto una curva che rappresenta il percorso di una montagna. Dividiamo l’intervallo lungo l’asse delle ascisse x in segmenti uguali e tracciamo dei rettangoli al di sotto della curva, con la base di ogni rettangolo che coincide con un segmento e l’altezza che tocca la curva.

Esempio Parabola

Consideriamo la parabola $y = x^2$ nell’intervallo [0, 1]. Dividiamo questo intervallo in n parti uguali di lunghezza $\Delta x = \frac{1}{n}$ . La somma di Riemann può essere espressa come:

$S = \sum_{i=1}^{n} f(x_i) \Delta x$

dove $x_i$ è un punto nell’intervallo $[x_{i-1}, x_i]$ . In questo caso, possiamo scegliere $x_i = \frac{i}{n}$ . Quindi, il calcolo della somma di Riemann diventa:

$S = \sum_{i=1}^{n} \left( \frac{i}{n} \right)^2 \cdot \frac{1}{n} = \sum_{i=1}^{n} \frac{i^2}{n^3} = \frac{1}{n^3} \sum_{i=1}^{n} i^2$

Utilizzando la formula per la somma dei quadrati dei primi n numeri interi:

$\sum_{i=1}^{n} i^2 = \frac{n(n+1)(2n+1)}{6}$

otteniamo:

$S = \frac{1}{n^3} \cdot \frac{n(n+1)(2n+1)}{6} = \frac{(n+1)(2n+1)}{6n^2}$

Quando n tende a infinito, questa somma si avvicina all’integrale:

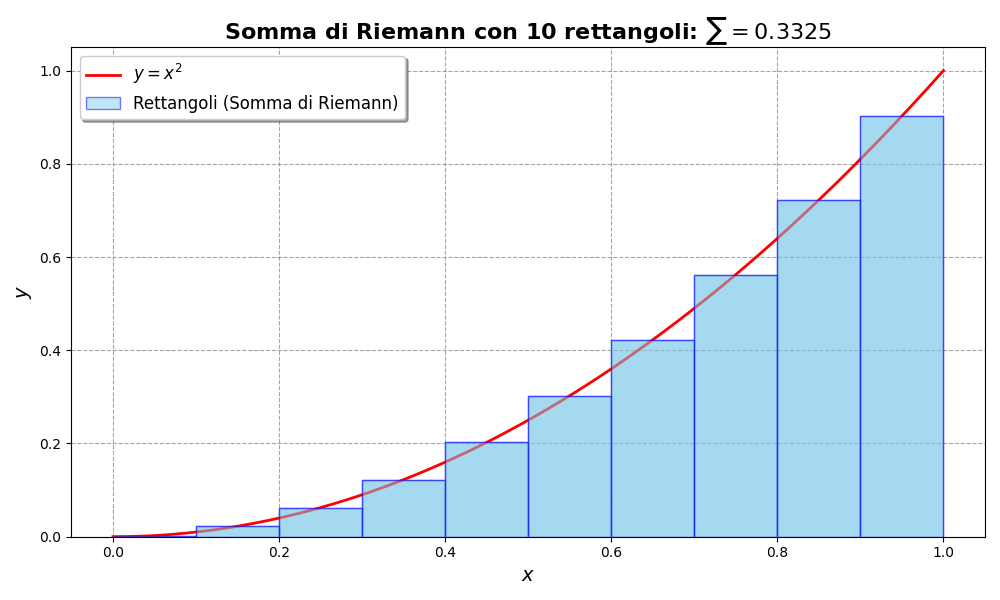
$\int_0^1 x^2 \, dx = \left[ \frac{x^3}{3} \right]_0^1 = \frac{1}{3}$

Grafico della Somma di Riemann per una Parabola

Per visualizzare meglio questo concetto, possiamo vedere come si comportano i rettangoli sotto la curva della parabola $y = x^2$ quando aumentiamo il numero di suddivisioni n sfruttando questo piccolo script personalizzabile ed eseguibile direttamente da browser su Python-Fiddle.

import matplotlib.pyplot as plt
import numpy as np

# Funzione della parabola
def f(x):
    return x**2

# Intervallo di integrazione
a, b = 0, 1
n = 10  # Numero di rettangoli

# Larghezza dei rettangoli
dx = (b - a) / n

# Punti di valutazione
x = np.linspace(a, b, n+1)
y = f(x)

# Sommando le aree dei rettangoli
x_mid = (x[:-1] + x[1:]) / 2
y_mid = f(x_mid)
sum_rectangles = np.sum(y_mid * dx)

# Creazione del grafico
x_vals = np.linspace(a, b, 1000)
y_vals = f(x_vals)

plt.plot(x_vals, y_vals, 'r', label='')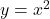
plt.bar(x_mid, y_mid, width=dx, alpha=0.5, edgecolor='b', label='Rettangoli (Somma di Riemann)')
plt.title(f'Somma di Riemann con {n} rettangoli: ')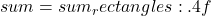
plt.xlabel('')
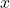plt.ylabel('')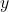
plt.legend()
plt.show()

HomeMade Experiment

Per i più curiosi, ecco un semplice esperimento che potete provare a casa. Disegnate una curva su un foglio di carta e dividete l’area sotto di essa in piccoli rettangoli, calcolandone le aree e sommandole. Confrontate poi questa somma con il risultato ottenuto utilizzando rettangoli più piccoli. Scoprirete quanto possa essere precisa questa tecnica e quanto affascinante sia la matematica!

La somma di Riemann ci insegna che anche le idee più semplici possono portare a grandi scoperte. La prossima volta che ammirerete un panorama o rifletterete su un problema complesso, ricordate che dietro ogni curva si nasconde una storia, e che la matematica è lo strumento che ci permette di raccontarla. Grazie per averci seguito in questo viaggio affascinante; alla prossima scoperta!

Ecco, cari lettori, una piccola finestra sulla meraviglia del pensiero matematico. Continuate a esplorare, a porvi domande e a lasciarvi affascinare dalle risposte che la scienza ha da offrire.

cyb3rdm0n